| Knot
theory
is
a
branch
of
mathematics
dealing
with
tangled
loops.
When
there's
just
one
loop,
it's
called
a
knot.
When
there's
more
than
one
loop,
it's
called
a
link
and
the
individual
loops
are
called
components
of
the
link.
A
picture
of
a
knot
is
called
a
knot
diagram
or
knot
projection.
A
place
where
parts
of
the
loop
cross
over
is
called
a
crossing.
The
simplest
knot
is
the
unknot
or
trivial
knot,
which
can
be
represented
by
a
loop
with
no
crossings. The
big
problem
in
knot
theory
is
finding
out
whether
two
knots
are
the
same
or
different.
Two
knots
are
regarded
as
being
the
same
if
they
can
be
moved
about
in
space,
without
cutting,
to
look
exactly
like
each
other.
Such
a
movement
is
called
an
ambient
isotopy
-
the
ambient
refers
to
moving
the
knot
through
3-dimensional
space,
and
isotopy
is
a
scary
word
from
topology
for
the
continuous
deformation
of
an
object
without
cutting
it
or
letting
it
pass
through
itself. Kurt
Reidemeister
showed
in
1932
that
any
diagram
of
a
knot
can
be
turned
into
any
other
diagram
of
the
same
knot
using
a
kit
of
3
moves
called
the
Reidemeister
Moves.
Unfortunately,
for
the
purposes
of
working
out
whether
two
knots
are
the
same,
it
can
take
an
enormous
number
of
Reidemeister
moves
to
get
from
one
diagram
to
another.
Any
attempt
to
untangle
the
Monster
diagram
with
Reidemeister
moves
involves
a
temporary
increase
in
the
number
of
crossings. A
special
case
of
working
out
whether
two
knots
are
the
same
is
the
problem
of
working
out
whether
a
given
knot
is
the
unknot.
Wolfgang
Haken
devised
a
procedure
in
1954,
published
in
1961,
but
it
takes
an
enormous
amount
of
effort
for
any
but
the
simplest
inputs
[Hass99]. An
excellent
introductory
book
for
knot
theory
is
[Adams94].
A
good
on-line
introduction
is
ThinkQuest
Knot
Theory.
A
comprehensive
page
of
high-quality
sites
is
Peter
Suber's
Knot
Links. Old
papers
I'm
typing
up- [Adams94]
Colin
C.
Adams.
The
Knot
Book
-
An
Elementary
Introduction
to
the
Mathematical
Theory
of
Knots.
W.
H.
Freeman
and
Company,
New
York,
1994.
- [Hass99]
Joel
Hass,
Jeffrey
C.
Lagarias,
Nicholas
Pippenger.
The
Computational
Complexity
of
Knot
and
Link
Problems.
Journal
of
the
ACM,
Vol.
46,
No.
2
(March
1999),
p.185
[Postscript
preprint]
| | A link with two
components | |
| | | | The
Unknot,
the
simplest
knot,
can
be
drawn
with
no
crossings | |
| | | | The Monster -
a
diagram
of
the
unknot.
Can
you
untangle
it?
Give up? | | | | | Trefoil
knots
-
these
can't
be
untangled
into
the
unknot,
and
the
two
mirror-image
versions
can't
be
deformed
into
one
another | | | | | | |
Type
II
Reidemeister
Move
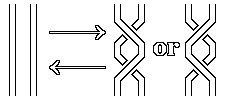 | |
Type
III
Reidemeister
Move
 | |
|