Number
Theory
Proofs | | Fred
Curtis
-
November
2000 |
| I
wrote
up
these
proofs
because
I
kept
misplacing
my
copy
of
Hardy
&
Wright,
and
when
it
wasn't
lost
the
proofs
it
contained
were
seemed
inaccessible
to
me. |
Cancellation
Law:
Can
cancel
a
in
ab = ac (mod m)
if
gcd(a, m) = 1
Proof:
If
ab = ac (mod m)
then
m | (ab-ac)
[defn
of
equality
mod
m],
i.e.
m | a(b-c).
If
gcd(a, m) = 1
then
m¬|a,
so
m | (b-c),
i.e.
b=c (mod m).
Note:
if
gcd(a, m) > 1
then
we
can't
always
cancel,
e.g.
2×1=2×4
(mod
6),
but
can't
cancel
the
2's
Proof:
If
p
is
prime
and
gcd(a,p) = 1
then
the
numbers
1a, 2a, ... (p-1)a
are
distinct
(mod p)
since
if
n1a = n2a (mod p)
then
n1 = n2 (mod p)
by
the
Cancellation
Law.
Since
none
of
1a, 2a, ... (p-1)a
are
zero (mod p)
and
there
are
only
(p-1)
distinct
non-zero
numbers
(mod
p),
the
numbers
1a, 2a, ... (p-1)a
must
be
congruent
to
1, 2, ... p-1
in
some
order.
Multiply
all
these
congruences
together
to
get:
| a·2a·...·(p-1)a | = | 1·2·...·(p-1) (mod p) | | ap-1(p-1)! | = | (p-1)! (mod p) | | ap-1 | = | 1 (mod p) |
(since
gcd((p-1)!, p) = 1
the
Cancellation
Law
applies.
Core
of
proof
shamelessly
stolen
from
[PS1]) | | a | 2a (mod 5) | 3a (mod 5) | 4a (mod 5) |
|---|
| 1 | 2 | 3 | 4 | | 2 | 4 | 1 | 3 | | 3 | 1 | 4 | 2 | | 4 | 3 | 2 | 1 |
| a | a2 (mod 5) | a3 (mod 5) | a4 (mod 5) |
|---|
| 1 | 1 | 1 | 1 | | 2 | 4 | 3 | 1 | | 3 | 4 | 2 | 1 | | 4 | 1 | 4 | 1 |
|
Euler's
Theorem:
aphi(m) = 1 (mod m)
if
gcd(a, m) = 1
| Euler's
Theorem
is
a
generalization
of
Fermat's
Little
Theorem
and
the
proof
presented
here
has
the
same
form
as
the
proof
presented
above
for
Fermat's
Little
Theorem.
phi(m)
denotes
the
number
of
positive
integers
less
than
m
which
are
relatively
prime
to
m.
For
prime
m,
phi(m)
=
m-1
and
we
have
the
special
case
of
Fermat's
Little
Theorem. Proof:
Let
r1, r2, ... rphi(m)
be
the
set
of
phi(m)
integers
less
than
m
and
relatively
prime
to
m.
If
gcd(a,p) = 1
then
the
numbers
r1a, r2a, ... rphi(m)a
are
distinct
(mod m)
since
if
ria = rja (mod m)
then
ri = rj (mod m)
by
the
Cancellation
Law.
Since
each
ria
is
relatively
prime
to
m
and
there
are
only
phi(m)
distinct
numbers
relatively
prime
to
m,
the
numbers
r1a, r2a, ... rphi(m)a
must
be
congruent
to
r1, r2, ... rphi(m)
in
some
order.
Multiply
all
these
congruences
together
to
get:
| r1a·r2a·...·rphi(m)a | = | r1·r2·...·rphi(m) (mod m) | | aphi(m)·r1·r2·...·rphi(m) | = | r1·r2·...·rphi(m) (mod m) | | aphi(m) | = | 1 (mod m) |
(since
gcd(r1·r2·...·rphi(m), m) = 1
the
Cancellation
Law
applies) | | a | 5a (mod 12) | 7a (mod 12) | 11a (mod 12) |
|---|
| 1 | 5 | 7 | 11 | | 5 | 1 | 11 | 7 | | 7 | 11 | 1 | 5 | | 11 | 7 | 5 | 1 |
phi(12)
=
4 | a | a2 (mod 12) | a3 (mod 12) | a4 (mod 12) |
|---|
| 1 | 1 | 1 | 1 | | 5 | 1 | 5 | 1 | | 7 | 1 | 7 | 1 | | 11 | 1 | 11 | 1 |
|
Wilson's
Theorem:
(n-1)! = -1 (mod n)
if
and
only
if
n
is
prime
[Also
known
as
Fermat's
Christmas
Theorem]
Case
1:
n
is
prime
Apart
from
1
and
-1
which
satisfy
x = x-1 (mod n),
all
the
numbers
from
1
to
n-1
may
be
grouped
in
pairs
satisfying
x = y-1
where
x
and
y
are
distinct.
So
| (n-1)! | = | 1·2·...·(n-1) |
| = | 1·...pairs
of
numbers
which
multiply
to
give
1 (mod n)...·(n-1) |
| = | 1·-1 (mod n) |
| = | -1 (mod n) |
Case
2:
n
is
composite
If
n = 4
then
(n-1)! = 6 = 2 (mod n).
If
n > 4
then
let
n = PQ
for
some
P > 1
and
Q > 1.
- If
P ¬= Q
then
both
P
and
Q
occur
in
1..(n-1),
so
n | (n-1)!,
i.e.
(n-1)! = 0 (mod n).
- If
P = Q
then
n = P2
and
both
P
and
2P
occur
in
1..(n-1),
so
n | (n-1)!,
i.e.
(n-1)! = 0 (mod n).
Proofs
of
this
theorem
are
many
and
often
tortuous.
The
theorem
pops
out
naturally
from
a
study
of
Gaussian
Integers,
but
it's
comforting
to
find
a
proof
using
simpler
techniques.
The
elegant
p=a2+b2
existence
proof
is
taken
almost
verbatim
from
[Nott].
The
uniqueness
proof
comes
from
[Burton]
p.307.
- If
p
prime
and
p=a2+b2
or,
more
generally,
if
a2 + b2 = 0 (mod p)
and
neither
a
nor
b
is
0 (mod p)
then
some
i2 = -1 (mod p)
| Proof: | a2 | = | -b2 | (mod p) | | a2/b2 | = | -1 | (mod p)
[neither
a
or
b
is
zero] | | (a/b)2 | = | -1 | (mod
p) | | Set
i
=
a/b,
then
i2 = -1 (mod p) |
- If
p
prime
and
some
i2 = -1 (mod p)
then
p=a2+b2
for
some
a,b
Proof:
Choose
k=floor(sqrt(p)),
so
k2 < p < (k+1)2.
The
list
of
numbers
x+iy
where
0 < x < k,
0 < y < k
contains
(k+1)2 > p
numbers,
but
there
are
only
p
distinct
numbers
(mod
p)
so
some
two
of
them
must
be
equal
(mod
p),
say
x1 + y1i = x2 + y2i (mod p)
for
distinct
pairs
(x1,y1)
and
(x2,y2).
Then| | x1-x2 | = | i(y2-y1) (mod p) | | (x1-x2)2 | = | -(y2-y1)2 (mod p) | | (x1-x2)2 + (y2-y1)2 | = | 0 (mod p) |
Set
a = |x1-x2|,
b = |y1-y2|
so
a2 + b2 = 0 (mod p).
But
0 < a2 + b2 < 2k2 < 2p
so
the
only
solution
is
a2 + b2 = p.
- If
p
prime
and
p=a2+b2
for
some
a,b
then
the
solution
is
unique
Proof:
Suppose
a2 + b2 = p = c2 + d2.| Then
a2d2 - b2c2 | = | a2d2 + b2d2 - b2d2 + b2c2 | | | = | (a2 + b2)d2 - (d2 + c2)b2 | | | = | pd2 - pb2 | | | = | p(d2 - b2) | | | = | 0 (mod p) | | (ad + bc)(ad - bc) | = | 0 (mod p) |
So
p | (ad - bc)
or
p | (ad + bc).
0 < a,b,c,d < sqrt(p)
implies
ad - bc = 0
or
ad + bc = p. | Case
1:
ad - bc = 0 | | ad = bc.
Since
a | bc
and
gcd(a,b)=1
we
have
a | c,
say
c = ka.
Then
ad = bc = bka,
i.e.
d = ka.
Then
p = c2 + d2=k2(a2 + b2),
so
k = 1,
a = c
and
b = d. | | Case
2:
ad + bc = p | | | p2 = | (a2 + b2)(c2 + d2) | | = | (ad + bc)2+(ac - bd)2 | | = | p2+(ac - bd)2 | | So
ac = bd
and,
by
an
argument
similar
to
case
1,
a = d
and
b = c. |
In
either
case,
the
pairs
(a,d)
and
(b,c)
are
the
same,
so
the
solution
to
a2 + b2 = p
is
unique.
- Prime
p = 1 (mod 4)
or
p = 2
<=>
some
i2 = -1 (mod p)
Proof:| If
p
is
a
prime
with
p = 3 (mod 4)
then
there
is
no
solution
to
p = a2 + b2
from
the
table
to
the
right,
and
from
step
2
above
no
solution
to
i2 = -1 (mod p). If
p = 2
then
12 = -1 (mod p). If
p
is
a
prime
with
p = 1 (mod 4)
then | | (p-1)! | = | 1 · 2 · ... · (p-2) · (p-1) (mod p) | | | = | 1 · 2 · ... · (p-1)/2 · -((p-1)/2) · ... · -2 · -1 (mod p) | | | = | ((p-1)/2)! · ((p-1)/2)! · -1(p-1)/2 (mod p) |
Since
p = 1 (mod 4),
(p-1)/2
is
even,
-1(p-1)/2 = 1
and
(p-1)! = ((p-1)/2)!2 (mod p),
but
(p-1)! = -1 (mod p)
by
Wilson's
Theorem.
Setting
i = ((p-1)/2)!
satisfies
i2 = (p-1)! = -1 (mod p). | |
| |
Proof:
If
a2 + b2 = 0 (mod p)
then
a2 = -b (mod p).
a = 0 (mod p)
and
b = 0 (mod p),
otherwise
we
could
write
(a/b)2 = -1 (mod p),
but
there
is
no
solution
to
i2 = -1 (mod p)
for
prime
p = 3 (mod 4).
This
result
is
usually
stated
in
textbooks
counting
negatives
and
reordering
as
separate
representations,
so
e.g.,
5 = 12 + 22 = 22 + 12 = -12 + 22 = -12 + -22 = ...,
a
total
of
8
representations.
This
makes
sense
if
you
want
to
count
the
number
of
lattice
points
5
units
from
the
origin,
but
it
can
be
a
nuisance
otherwise.
The
discussion
here
treats
these
representations
as
equivalent,
so
e.g.
5 = 12 + 22
(5
can
be
written
as
the
sum
of
two
squares
in
1
way
only),
65 = 12 + 82 = 72 + 42
(65
can
be
written
as
the
sum
of
two
squares
in
2
ways).
Let
numsq(n)
denote
the
number
of
ways
a
number
n
can
be
written
as
the
sum
of
two
squares.
Factor
n
as
n = 2rPQ
where
r > 0,
P
is
a
product
of
primes
equal
to
1 (mod 4),
Q
is
the
product
of
primes
equal
to
3 (mod 4).
| numsq(n)
= | 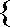 | 0
if
Q
is
not
a
square |
| numsq(P)
if
Q
is
a
square |
Proof:
If
n = a2 + b2,
prime
q = 3 (mod 4),
q | n
then
q | a,
q | b
and
q2 | n.
This
reduces
to
a
smaller
case
n / q2 = (a / q)2 + (b / q)2.
Continued
reduction
removes
primes
equal
to
3 (mod 4)
in
pairs,
so
any
sum-of-squares
solution
of
n
corresponds
one-to-one
to
a
sum-of-squares
solution
of
n / Q = 2rP
if
Q
is
a
square,
or
yields
a
contradiction
[implying
numsq(n) = 0]
if
Q
is
not
a
square.
So
if
Q
is
a
square,
numsq(n) = numsq(2rP).
If
r > 2
then
2rP = 0 (mod 4),
and
[by
Table:
Sums
of
squares
modulo
4]
2 | x
and
2 | y,
so
numsq(2rP) = numsq(2r-2P).
Case
1:
If
r
is
even,
then
numsq(n) = numsq(2rP) = numsq(P)
as
required.
Case
2:
If
r
is
odd,
then
numsq(n) = numsq(2rP) = numsq(2P).
Now,
2P = 2 (mod 4)
so
any
solution
to
2P = x2 + y2
has
x
and
y
odd.
Now,
((y + x) / 2)2 + ((y - x) / 2)2 = (x2 + y2) / 2 = 2P / 2 = P,
i.e.
each
sum-of-squares
solution
of
2P
corresponds
one-to-one
to
a
sum-of-squares
solution
of
P
and
numsq(n) = numsq(2rP) = numsq(2P) = numsq(P)
as
required.
-
To
be
completed:
proof
for
value
of
numsq(P)
where
P
is
a
product
of
primes
equal
to
1 (mod 4
| n | n2
(mod
17) | n2
(mod
17) | n |
|---|
| ±1 | 1 | -1 | ±4 | | ±6 | 2 | -2 | ±7 | | ±2 | 4 | -4 | ±8 | | ±5 | 8 | -8 | ±3 |
| | | n | n2 (mod 19) | n2 (mod 19) | n |
|---|
| ±1 | 1 | -2 | ±6 | | ±4 | -3 | 4 | ±2 | | ±9 | 5 | 6 | ±5 | | ±8 | 7 | -8 | ±7 | | ±3 | 9 | | |
|
- [Burton]
-
"Elementary
Number
Theory"
by
David
M.
Burton,
2nd
edn,
University
of
New
Hampshire.,
1989.
- [Hardy
&
Wright]
-
"An
Introduction
to
the
Theory
of
Numbers"
by
G.H.
Hardy
and
E.M.
Wright,
Oxford
University
Press,
1938.
- [Nott]
-
"G13NUM:
Number
Theory"
-
Course
notes
from
the
School
of
Mathematical
Sciences,
University
of
Nottingham.
- [PS1]
-
WWW
page:
Fermat's
Little
Theorem
from
the
Prime
Site's
list
of
proofs