| Bemerkungen
zur
Knotentheorie
(Remarks
on
Knot
Theory)Von
LEBRECHT
GOERITZ
in
Rostock | |
| §1.
Eine
Bemerkung
zu
en
Kreisprojektionen | | §1.
A
Remark
on
Knot
Diagrams | |
| ¶1 | Bekanntlich
läßt
sich
jede
alternierende
Kreisprojektionen
als
solche
erkennen;
bei
nichtalternierenden
Projektionen
gibt
es
ein
solches
Verfahren
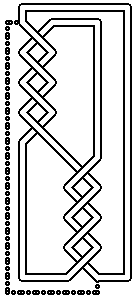
nicht. |  | | Fig.
1. |
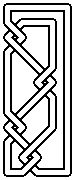
 | | Fig.
2. |
| As
is
well
known,
an
alternating
knot
diagram
can
be
recognised
as
such;
for
a
non-alternating
diagram
there
is
no
such
procedure. | |
| Man
kann
daher
die
Frage
aufwerfen
worin
die
Schwierigkeit
dieser
Entscheidung
begründet
ist. | One
can
therefore
raise
the
question
where
the
difficulty
of
this
decision
is
substantiated. | |
Note
§1 ¶1 | Dieselbe
wird
durch
die
bemerkenswerte
Tatsache
beleuchtet,
daß
man
allein
bei
Anwendung
der
in
der
Knotentheorie[1]
I,
§3,
erklärten
Operationen
?Omega?;i
.upidx
?(")
(i=1,2,3)
und
?Omega?;3,
d.
h.
ohne
in
der
Projektion
vorher
neue
Doppelpunkte
einzuführen. | This
question
is
illuminated
by
the
remarkable
fact
that
just
applying
the
operations
?Omega?;i
.upidx
?(")
(i=1,2,3)
and
?Omega?;3
from
Knotentheorie[1]
I,
§3,
i.e.
without
introducing
new
crossings
beforehand
into
the
diagram. | Note
§1 ¶1 |
| im
allgemeinen
bei
einer
Kreisprojektion
nicht
alle
Doppelpunkte
herausschaffen
kann.
| In
general,
not
all
crossings
can
be
removed
from
a
knot
diagram.
| |
| ¶2 | Die
in
Figur
1
angegebene
Projektion
gestattet
an
keiner
Stelle
die
Anwendung
einer
der
Operationen
?Omega?;i
.upidx
?(")
oder
?Omega?;3.
Nimmt
man
noch
die
in
I.
§5,
der
Knotentheorie
erklärte
Operation
?Omega?;5
hinzu,
so
kann
man
alle
Doppelpunkte
ohne
Hinzunahme
neuer
herausschaffen. | The
diagram
in
figure
1
permits
none
of
the
operations
?Omega?;i
.upidx
?(")
or
?Omega?;3.
If
one
adds
the
operation
?Omega?;5
from
Knotentheorie
I.
§5,
then
one
can
once
again
remove
all
crossings. | |
| ¶3 | Daß
es
auch
Kreisprojektionen
gibt,
die
sich
ohne
Einführung
neuer
Doppelpunkte
auch
bei
Zuhilfenahme
der
Operationen
?Omega?;i,
?Omega?;k
.upidx
?(")
(i=3,4,5;
k=1,2,3,4,5)
nicht
vereinfachen
lassen,
lehrt
die
Figur
2. | Figure
2
shows
that
even
with
the
help
of
operations
?Omega?;i,
?Omega?;k
.upidx
?(")
(i=3,4,5;
k=1,2,3,4,5)
there
are
knot
diagrams
left
unsimplified
without
the
introduction
of
new
crossings. | |
|
| | [1] | K.
Reidemeister,
Knotentheorie,
Ergebnisse
der
Mathematik,
Bd.
1. An
English
translation
was
published:
Knot
theory
by
Kurt
Reidemeister
;
translated
from
the
German
and
edited
by
Leo
F.
Boron,
Charles
O.
Christenson,
and
Bryan
A.
Smith.
Moscow,
Idaho,
U.S.A.
:
BCS
Associates,
1983. |
|
| |
| §2.
Zur
Berechnung
der
C;p | | §2.
Calculating
C;p | |
| ¶1 | Die
in
der
Knotentheorie
S. 29
angegebene
Berechnungsvorschrift
der
C;p
verlangt
die
Transformation
einer
quadratischen
Form | | The
rule
for
calculating
C;p
(Knotentheorie,
§8,
page
29)
requires
the
transformation
of
a
quadratic
form | |
| f(x)
=
'Sum((a;ik)*(x;i)*(x;k),
'tuple(i,k),
1,
n) | |
| mit
ganzen
rationalen
Koeffizienten
a;ik
und
von
Null
verschiedener
Determinante
a;ik
!=
0
in
die
Form | | with
whole
rational
coefficients
a;ik
and
of
non-zero
determinant
a;ik!
=
0
into
the
form | Note
§2 ¶1 |
| g(y)
=
'Sum((b;i)*(y;i)^2,
i,1,
n). | |
This
effort
is
hampered
by
my
almost
total
ignorance
of
German.
The
English
rendering
presented
here
is
not
a
faithful
translation
-
my
aim
is
to
capture
the
meaning
of
Goeritz'
words.
Attempts
have
been
made
to
modernise
some
terms:
Kreisprojektionen
is
rendered
"[knot]
diagram",
Doppelpunkte
as
"crossing"
etc.
