-Up to-Home/Maths/Knot Theory
-Site Map

Concise encoding of link diagrams

   http://arxiv.org/abs/math/???????
8th December, 2001
Fred Curtis, Dept. Inapplicable Mathematics, Miskatonic University, Arkham, MA 65261. 
Abstract: Two unambiguous encoding schemes for link diagrams are given:
a dowker-like scheme suitable for use by humans and a space-efficient scheme
taking 5 bits per crossing and admitting various canonical forms.		 
 
 
 

Motivation

In the study of link diagrams, as opposed to the underlying links they represent, it is convenient to encode diagrams as symbol strings, e.g. to communicate diagrams via text messages or for machine storage & manipulation of diagrams. Dowker-Thistlethwaite notation [Adams94 §2.2] can represent knots but its strength - abstracting away the vagaries of diagrams and concentrating on the underlying knot - means that diagrams cannot be unambiguously recovered, e.g. the two unknot diagrams in Fig. 1 are distinct (whether considered on the plane or sphere) yet have the same notation. Two encoding schemes are presented for connected link diagrams: a simple Dowker-like encoding which may be performed manually by humans and a space-efficient scheme taking 5 bits per crossing.
knot:(97411'48633697'426)22(411'48633699'62477)
Fig. 1

Manual encoding

Encode a connected link diagram thus:
  1. Number or otherwise label each crossing in the link diagram.
  2. Shade alternating regions in the link diagram.
  3. For each shaded region, write the labels around the region in counter-clockwise order, separating the labels for each region by a "/". The first time a label is written, prefix it by a sign according to the convention in Fig 2; the arrows are taken to lie in the shaded region and indicate the counter-clockwise traversal.
-
Fig 2.
Example:Step 1:
-		Step 2:
-		Step 3: Encoding is:

-4, -3, -2, -1 /
-5, 4 /
5, +8, +9 /
9, +7, 8 /
+6, 7 /
6, 1, 2, 3

A diagram is reconstructed from an encoding as follows:

Encoding a link diagram via a signed planar map

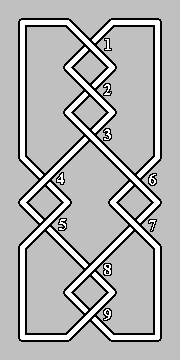
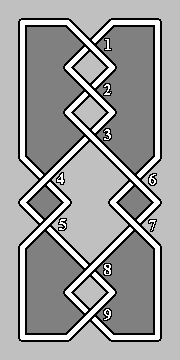
A connected link diagram can be represented as a signed planar graph [Adams94, §2.4, §7.4]. The term planar graph is misleading since, in the context of link diagrams, a particular graph embedding is required. While 3-connected planar graphs have essentially only one embedding, planar graphs in general may have multiple embeddings. The link diagrams in Fig. 3, for example, are distinct (consider the number of crossings in each which may be removed by a type I Reidemeister move) but have the same signed planar graphs. For this reason, the term signed planar map is preferred.

In a signed planar map corresponding to a connected link diagram, each edge in the map corresponds to a crossing in the link diagram. An arbitrary connected finite planar map can be encoded using 4 bits per edge [Curtis01a], so a link diagram can be encoded using 5 bits per crossing by converting it to a signed planar map and then appending sign bits for the edges in some suitable order, e.g. by first occurence of each edge in the counter-clockwise traversal of the intermediate tree described in the encoding phase.

The link diagram can be recovered from the encoding by recovering map as per [Curtis01a], restoring the edge signs from the appended sign bits and converting the signed planar map back into a link diagram.

knot:(4796247'96333'68411447789966321'1)333(44414863'214863'666874269'8)
Fig 3.

References

-This page
last changed:
12 Dec 2001
[Validate HTML]
-Donate free
food & land		 
-
|Feedback by email
or Web form